Solution of Non Linear Partial Differential Equations
Project Abstract
The numerical solution of nonlinear partial differential equations (PDEs) is crucial in various scientific and engineering fields. In this study, we implemented Newton’s Method, Quasi-Linearization Method, and the Finite Difference Method (FDM) to solve different types of nonlinear PDEs, including the Burgers’ equation. The Newton-Raphson scheme was utilized to convert nonlinear PDEs into a system of linear equations, which were then solved using iterative techniques. Similarly, the Quasi-Linearization Method was applied to linearize nonlinear PDEs for efficient computation. The implementation was carried out using Python, leveraging numerical techniques to ensure accuracy, stability, and computational efficiency. The results demonstrate the effectiveness of these methods in handling nonlinear PDEs, providing valuable insights into their numerical behavior and practical applications.
Project Supervisor
Dr. Harshita Madduri ( Assistant Professor, Department of Mathematics NIT Kurukshetra )
Key Features
-
Applied Newton’s Method, Quasi-Linearization Method, and Finite Difference Method (FDM) to solve nonlinear PDEs.
-
Used Newton-Raphson Scheme to transform nonlinear PDEs into a system of linear equations for efficient solving.
-
Solved and analyzed Burgers’ equation as a case study for nonlinear PDEs.
-
Utilized Python with NumPy and SciPy for numerical computations and efficient solution strategies.
-
Ensured numerical stability while maintaining high accuracy in solving nonlinear PDEs.
-
Evaluated the effectiveness of different numerical approaches in handling nonlinear PDEs.
-
Applicable to fluid dynamics, financial modeling, and engineering problems where nonlinear PDEs arise.
Newton's Method

Example

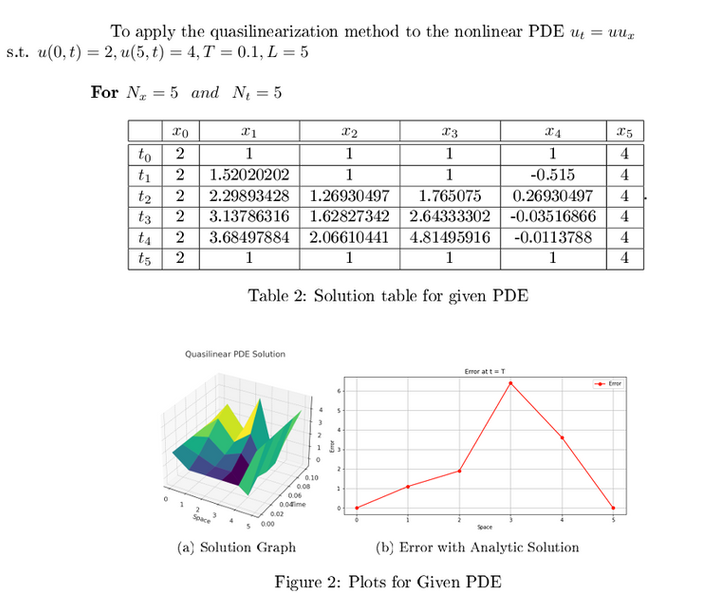
Solution of PDE using Newton's Scheme