Comparison of Solution of Parabolic PDEs
Project Abstract
The numerical solution of the Heat Equation plays a crucial role in various scientific and engineering applications. In this study, we implemented Explicit, Implicit, and Crank-Nicholson schemes to solve the Heat Equation and performed a comparative analysis of their computational costs. To efficiently solve the resulting Tri-Diagonal System of Linear Equations (SOLE), we employed the Thomas Algorithm and Sparse Matrix methods, ensuring optimal computational efficiency. The implementation was carried out using Python, with a focus on accuracy, stability, and performance. The comparative results highlight the trade-offs between different schemes in terms of convergence, stability, and computational complexity, providing valuable insights for selecting the most appropriate method for practical applications.
Project Supervisor
Dr. Harshita Madduri ( Assistant Professor, Department of Mathematics NIT Kurukshetra )
Key Features
-
Implemented Multiple Numerical Schemes
-
Efficient SOLE Solver
-
Computational Cost Analysis
-
Python-Based Implementation
-
Optimized Performance
-
Real-World Applicability
Parabolic Equation Model

Numerical Scheme



Example

Solution

Example

Solution
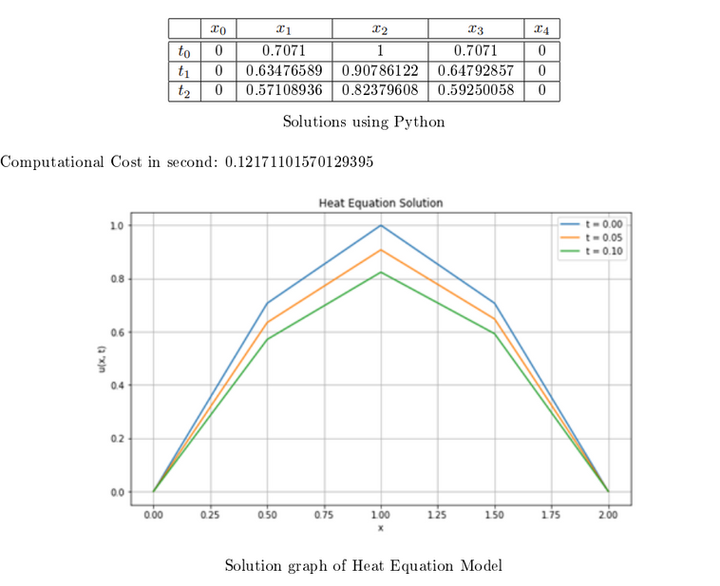
Example
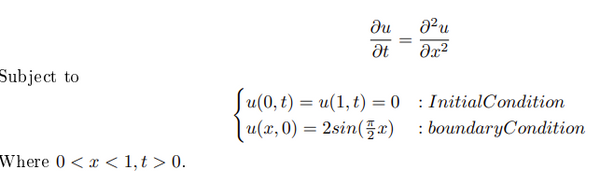
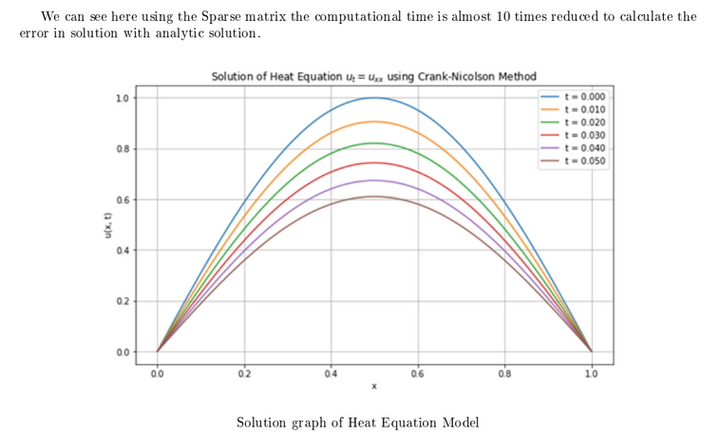
Solution

Stability Condition for Explicit Method
